La dimension fractale, une autre caractéristique des images fractales Les fractales sont des courbes à dimensions infinies sur un espace fini. C'est là qu'est la clé de la dimension fractale. Ce n'est plus un nombre entier.

Comment mesureriez vous la longueur de la côte Bretonne ?

Prenons le littoral atlantique des Etats Unis. Sur un Atlas il paraîtrait être entre trois et six mille kilomètres de long dépendamment du niveau de détail de la carte du monde que l'on utilise. Un morceau du littoral à plus petite échelle montrerait de plus grandes baies, ce qui rendrait la longueur de la côte plus grande alors que la distance entre les points nord et sud limitrophes du littoral Atlantique Américain n'a pas changé. Un être humain ne pourrait pas enjamber toutes les rentrées d'eau, il faudrait qu'il contourne les baies et il aurait besoin de marcher une distance bien plus grande que celle indiquée sur la carte. Une fourmi devrait contourner encore plus de baies que l'être humain, et parcourir ainsi une distance encore plus grande. Encore une fois la distance entre le point a et le point b n'a pas changé, c'est le niveau de détails qui a changé. Imaginons qu'un électron fasse le même voyage, il aurait besoin de manœuvrer entre tous les atomes de la terre, du sable d'un coté et ceux de l'eau de l'autre, il ferait des milliers de millions de tours et détours, et ne pourrait pas parcourir la côte aussi facilement que la fourmi l'avait difficilement réalisé auparavant. En supposant que la nature soit infiniment détaillée le littoral entre le point a et b est infini. Alors que la surface entourée d'eau est finie. Le littoral existe en dimension fractale.

En mathématiques, il était généralement accepté que des objets existaient soit en 0 (le point), 1(la droite), 2(le carré, la section d'un plan), ou 3(les cubes, les sphères) dimensions. Au début du siècle un mathématicien qui s'appelait Cantor a imaginé un curieux objet construit de manière récursive. Il a pris un segment de longueur x. Il a sorti le tiers du milieu en premier puis a divisé les segments restants en trois en sortant encore le tiers du milieu… et ainsi de suite. Si on continuait de faire ça encore et encore, à l'infini, on n'obtiendrait pas un nombre fini d'ensembles à zéro dimension. Il y en aurait un nombre infini, et ce ne serait pas des points mais des bouts de ligne coupés à des longueurs d'infini petitesse…..Cette collection de points aléatoires n'est pas non plus de dimension 1, puisqu'on l'avait coupé une infinité de fois et une infinité d'itérations de ce type ne pourrait pas créer quoi que ce soit ayant une longueur….Quelle est la dimension de cet objet ?

Le diagramme suivant nous montre comment considérer les dimensions comprises entre 1 et 2, les dimensions fractales. En utilisant la courbe de Von Koch.

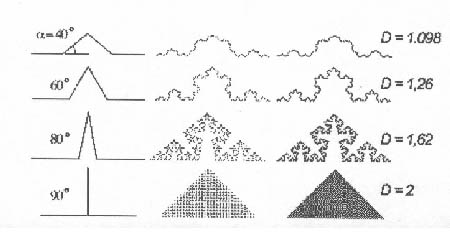
On a calculé D à partir de la formule mathématique suivante : D=log 2/log (2 cos ß/2).

Quand l'angle est 90°, le triangle est entièrement couvert, donc c'est une surface et sa dimension est 2. Si l'angle est 0°, on obtient une ligne de dimension 1. Entre les deux, on a des dimensions fractales.

Dans les nouvelles formes de mathématiques utilisant la 4ème dimension et les dimensions fractales, on voit un moyen de décrire les éléments chaotiques de la nature et de notre Univers.